例題
ある工場で製品1、製品2を生産します。製品1は原材料Aを1kg、原材料Bを3kg使用し8万円で売れます。また、製品2は原材料Aを1kg、原材料Bを1kg使用し6万円で売れます。原材料Aが4kg、原材料Bが6kgあるとき、製品1と製品2をいくつずつ作れば利益が最大になりますか?
| 製品1 | 製品2 | 在庫 | |
|---|---|---|---|
| 原材料A [kg] | 1 | 1 | 4 |
| 原材料B [kg] | 3 | 1 | 6 |
| 価格 [万円] | 8 | 6 |
解
製品1を$x_1$個、製品2を$x_2$個つくるとします。 この問題は
と書くことができます。
このような線形計画問題を解くアルゴリズムには、シンプレックス法や内点法があります。Pythonのscipyにはシンプレックス法によるソルバーがあります。以下でscipyによる計算結果を示します。
import numpy as np
from scipy.optimize import linprog
c = - np.array([8, 6])
aub = np.matrix([[1,1],[3,1]])
bub = np.array([4, 6])
bounds = np.array([0, None])
res = linprog(c, A_ub=aub, b_ub=bub, bounds=bounds)
得られた変数resは以下のようになります。
fun: -26.0
message: 'Optimization terminated successfully.'
nit: 2
slack: array([0., 0.])
status: 0
success: True
x: array([1., 3.])
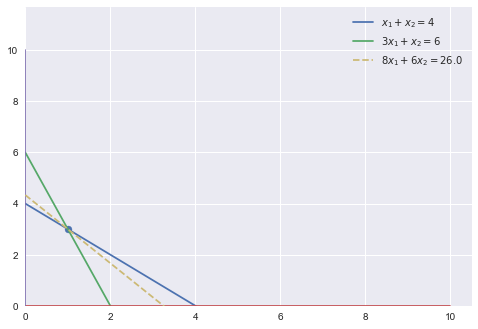
以下に可視化の結果を示します。
import matplotlib.pyplot as plt
import seaborn as sns
x1 = np.linspace(0, 10)
x2 = np.linspace(0, 10)
ub1 = 4 - x1
ub2 = 6 - 3 * x1
obj_val = -res.fun
obj = (obj_val - 8 * x1) / 6
plt.plot(x1, ub1, label='$x_1+x_2 = 4$')
plt.plot(x1, ub2, label='$3x_1+x_2 = 6$')
plt.plot(x1, x1 * 0)
plt.plot(x1 * 0, x2)
plt.plot(x1, obj,'--' ,label='$8x_1 + 6x_2 = '+str(obj_val)+'$')
plt.scatter(res.x[0], res.x[1])
plt.xlim(left=0)
plt.ylim(bottom=0)
plt.legend()
双対問題
線形計画問題では、双対問題を考えることで、計算が簡単になったり、問題の解釈や応用の見通しがよくなったりします。
双対定理 次のような主問題(P)に対する双対問題(D)
(P)
A x \geq b
x \geq 0 $$
(D)
{}^tA y \leq c
y \geq 0 $$
に対して、(P)、(D)に実行可能解が少なくともひとつずつ存在すると仮定します。このとき、(P)、(D)それぞれ最適解$x^*$、$y^*$が存在し、
$$
{}^tc x^* = {}^tb y^*
$$
が成り立ちます。
証明 双対定理の証明は、次の手順で示すことができます。
以下の弱双対定理を示す: 任意の実行可能解
$x$、$y$について$$ {}^tc x \geq {}^tb y \ . $$以下を示す:
$$ {}^tc x \leq {}^tb y $$を満たす実行可能解$x$、$y$が存在する。
この2つより、両方を満たすような$(\bar{x},\bar{y})$は${}^tc \bar{x} = {}^tb \bar{y}$であることが分かります。
さらに、もし${}^tc \bar{x} > {}^tc x$を満たすような$x$が存在するとしたら、それは${}^tc \bar{y} > {}^tc x$となり、1の弱双対定理に矛盾することから、$\bar{x}$が主問題の最適解であること、同様の議論から$\bar{y}$が双対問題の最適解であることが示せます。
1は不等式の変形から