ナイキストの安定判別法 (Nyquist stability criterion)は、簡単に閉ループ制御系の安定性を判別する方法です。ここでは、なぜナイキストの安定判別法が必要なのかを考えてから、ナイキストの安定判別法を導出してみます。
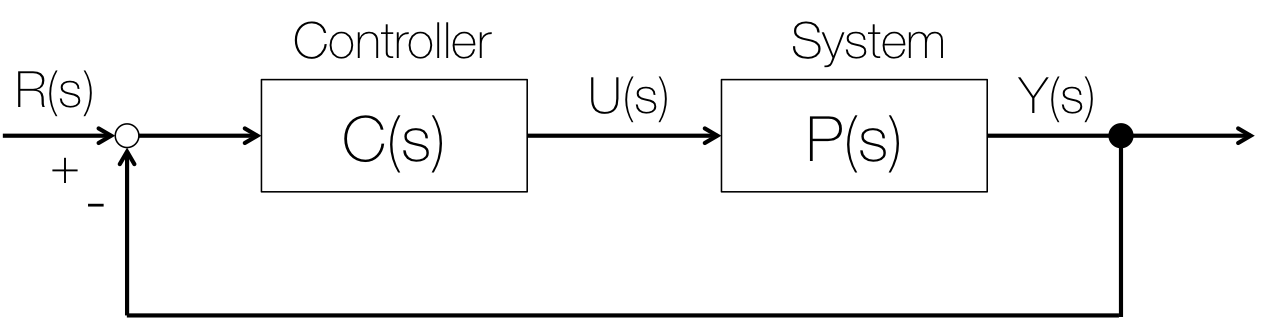
図1.閉ループ制御系
なぜナイキストの安定判別法が必要なのか
図1. のような一般の閉ループ制御系を考えます。この系の伝達関数 $G(s)$ は、
$$ G(s) := \frac{Y(s)}{R(s)} = \frac{P(s)C(s)}{1+P(s)C(s)} $$
です。この系が安定かどうかは極 ($1+P(s)C(s)=0$ の $s$ についての解) の符号を調べれば分かります(極と安定性の関係については こちら)。しかし、一般の多項式の複素解を手計算で求めるのは簡単ではありません。ではどうしたらいいでしょうか?ナイキストの安定判別法は極を求めずに、実部が正の極があるかどうかを調べることで、極を求める計算が難いので安定性が分からない、という問題を解決する方法なのです。
ナイキストの安定判別法の導出
ナイキストの安定判別法は、 $P(s)C(s)$ については、事前に設計したり、モデル化したりすることで分かっていることを利用します。
まず、 $P(s)C(s)$ の零点を $z_i,\cdots,z_m$ 、極を $p_1, \cdots p_n$ が分かっているとして、 $P(s)C(s)$ は
$$ P(s)C(s) = \frac{K(s-z_1)\cdots(s-z_m)}{(s-p_1)\cdots(s-p_n)} $$
と表すことができます。よって、特性方程式は
$$ 1+P(s)C(s)=\frac{(s-p_1)\cdots(s-p_n)+K(s-z_1)\cdots(s-z_m)}{(s-p_1)\cdots(s-p_n)} =0 $$
となります。さらに、特性方程式の零点を $r_1,\cdots,r_n$ とおけば、
$$ 1+P(s)C(s)=\frac{A(s-r_1)\cdots(s-r_n)}{(s-p_1)\cdots(s-p_n)} =0 $$
と表すことができます。ここで、伝達関数は
$$ \begin{align} G(s) &= \frac{P(s)C(s)}{1+P(s)C(s)} \\ &= \frac{K(s-z_1)\cdots(s-z_m)}{(s-p_1)\cdots(s-p_n)}\frac{(s-p_1)\cdots(s-p_n)}{A(s-r_1)\cdots(s-r_n)} \\ &=\frac{K(s-z_1)\cdots(s-z_m)}{A(s-r_1)\cdots(s-r_n)} \end{align} $$
となるので、特性方程式の零点 $r_1,\cdots,r_n$ は、伝達関数の極になっています。いま $1+P(s)C(s)$ の零点 $r_i,\cdots,r_n$ と極 $p_i,\cdots,p_m$ のうち、実部が正であるものの数をそれぞれ、 $R$ 、 $P$ とします。いまのところ、 $P$ は分かりますが、 $R$ は分かりません。
次に、図2(A)に示すように、複素平面において、右半平面全体を虚軸と半径無限大の円周で囲む閉曲線 $C$ を考えます。 $s$ を閉曲線 $C$ にそって、時計周りに1周させたときの $1+P(s)C(s)$ の軌跡 $\Gamma$ をプロットします。この $\Gamma$ が原点を中心に時計方向に回る回転数を $N$ とします。
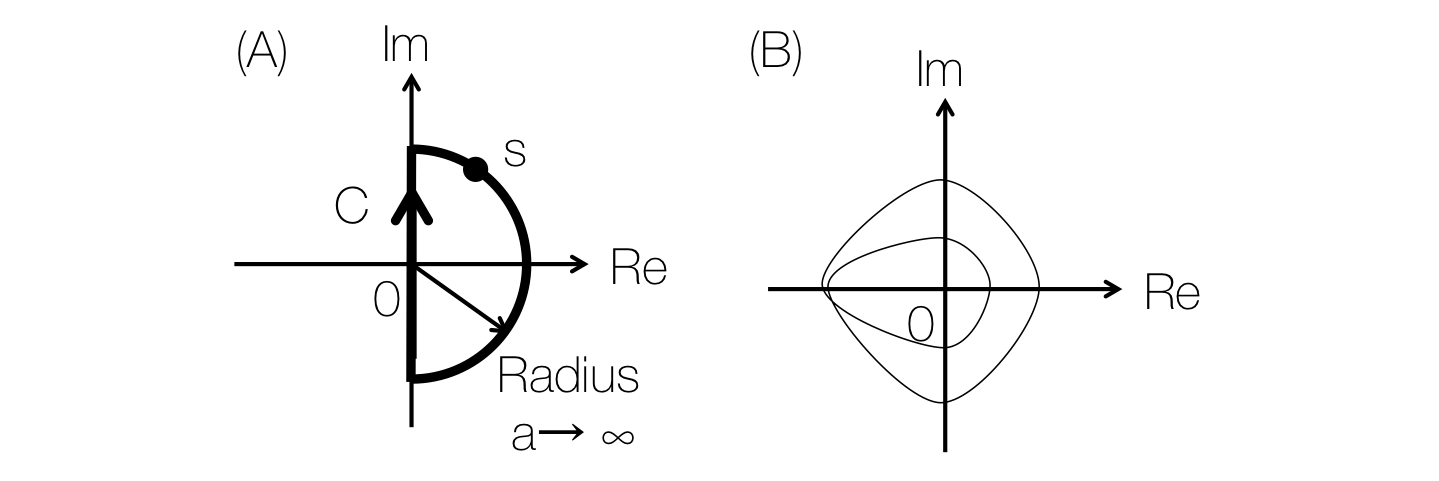
図2. (A) 閉曲線 $C$ (B)軌跡 $\Gamma$ (適当です) この場合 $N=2$
ここで、 複素数 $b_1:=c_1e^{i\theta_1}, b_2:=c_2e^{i\theta_2}$ を考えると、その積の位相は、
$$ \angle b_1b_2 = \angle c_1c_2 e^{i(\theta_1+\theta_2)} = \theta_1+\theta_2 = \angle b_1 + \angle b_2 $$
となり、それぞれの位相の和で表せることを使うと、$1+P(s)C(s)$ の位相 $\theta$ は式 () より、
$$ \theta = \sum_i^{n} \angle (s-r_i) - \sum_j^n \angle (s-p_j) $$
となります。 $s$ を閉曲線 $C$ にそって時計回りに1周させたとき、 $\angle (s-r_i)$ 、$\angle (s-p_i)$ がどう変化するかを考えると、 $r_i$ 、 $p_i$ の実部が正のときは、ベクトル $s-r_i$ 、 $s-p_i$ が時計周りに1回転し、そうでないときには、回転しないことが分かります。よって、その和である $\theta$ について考えると、 $1+P(s)C(s)$ が原点を中心に回転する数は、 実部が正である $r_i$ の個数 $R$ から、実部が正である $p_i$ の個数 $P$ をひいたものになります。すなわち、
$$ N = R + P $$
が成り立ちます。軌跡 $\Gamma$ のプロットから $N$ が分かり、 $P$ はもともと分かっているので、 $R$ が求めることができます! 改めて $R$ が何を表していたのか確認すると、伝達関数の極のうち、実部が正のものの個数でした。よって、閉ループ制御系は $R=0$ なら安定、 $R>0$ なら不安定です。
ここで、軌跡 $\Gamma$ をどう描いたらいいのか考えてみましょう。虚軸上の点は $s$ を $[-i\infty,i\infty]$ の間で動かせばいいでしょう。では、半径無限大の円周上の点はどうなるでしょうか。 $s=ae^{i\varphi}$ とすると、軌跡 $\Gamma(s)$ は
$$ \begin{align} \Gamma(s)& =\lim_{a\rightarrow\infty}1+P(s)C(s) \\ & =\lim_{a\rightarrow\infty} \frac{A(ae^{i\varphi}-r_1)\cdots(ae^{i\varphi}-r_n)}{(ae^{i\varphi}-p_1)\cdots(ae^{i\varphi}-p_n)}\\ & =A \end{align} $$
となり、結局閉曲線 $C$ 上で $s$ を動かしたときの軌跡は区間 $[-i\infty,i\infty]$ の間で動かしたときと変わらないことが分かります。
また、 $1+P(s)C(s)$ が原点を中心に回転する数は、$P(s)C(s)$ が複素平面上の点 $(-1,0)$ を中心に回転する数と等しいです。
これまでのことを整理すると、
- $P(s)C(s)$ の実部が正の極の数を $P$ とする
- $s=iw$ とし $P(iw)C(iw)$ の区間 $w \in [-\infty,\infty]$ での軌道 $\Gamma$ を描き、複素平面上の点 $(-1,0)$ を中心に時計回りに回転した数を $N$ とする
- $R=N-P$ を計算し、$R=0$ なら安定、 $R>0$ なら不安定
これがナイキストの安定判別法です。
誤りのご指摘等はTwitterまでお願いします。